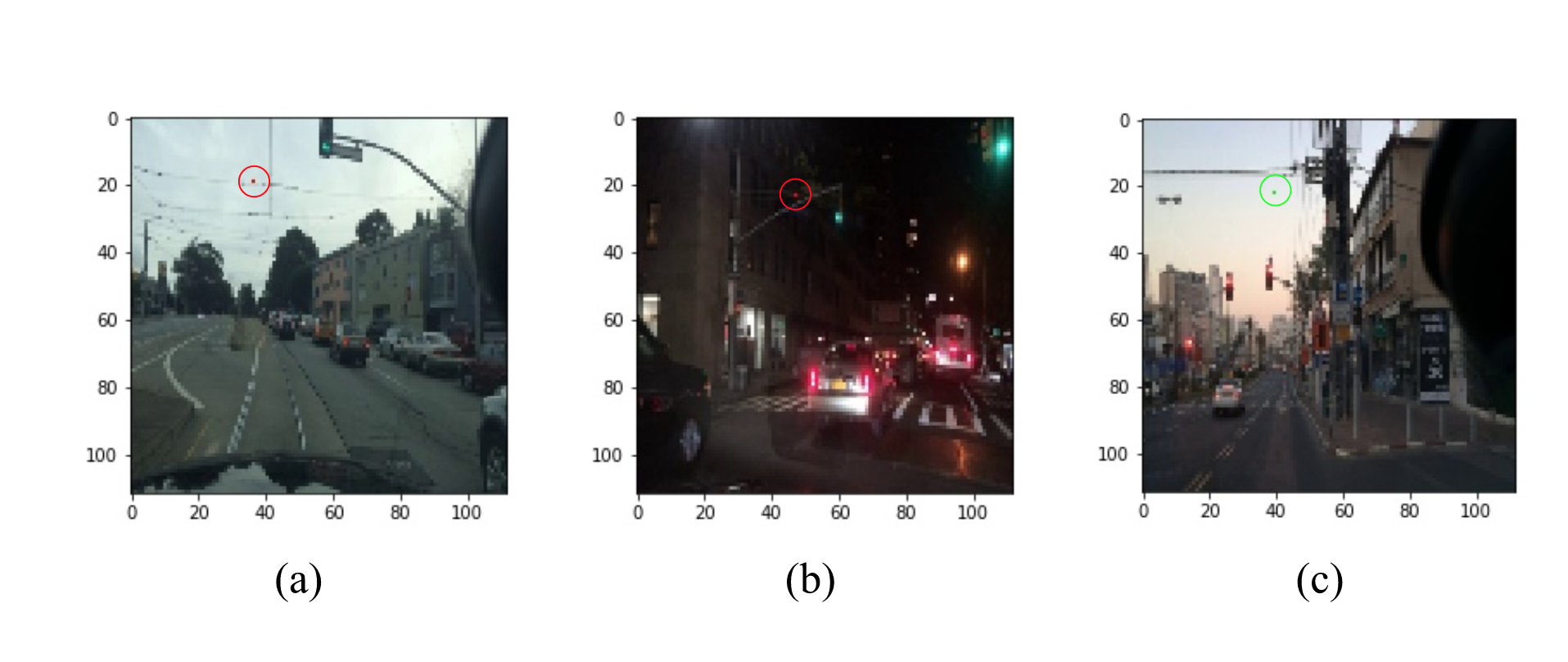
Adversarial examples. Neural networks lack robustness.

Machine learning – the science of building systems from data – is revolutionising computer science and artificial intelligence (AI). Much of its success is due to deep neural networks, which have demonstrated outstanding performance in perception tasks such as image classification. Solutions based on deep learning are now being deployed in a multitude of real-world systems, from virtual personal assistants, through automated decision making in business, to self-driving cars.

Deep neural networks have good generalisation properties, but are unstable with respect to so called adversarial examples, where a small, intentional input perturbation causes a false prediction, often with high confidence. Adversarial examples are still poorly understood but attracting attention because of the potential risks to safety and security in applications. The image shows a traffic light correctly classified by a convolutional neural network, which is then misclassified after changing only a few pixels. This illustrative example, though somewhat artificial, since in practice the controller would rely on additional sensor input when making a decision, highlights the need for appropriate mechanisms and frameworks to prevent the occurrence of similar robustness issues during deployment.

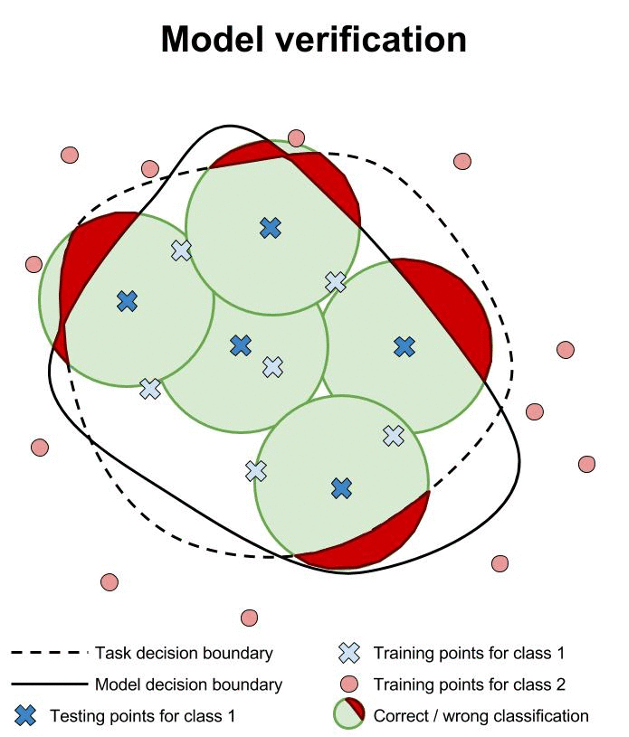
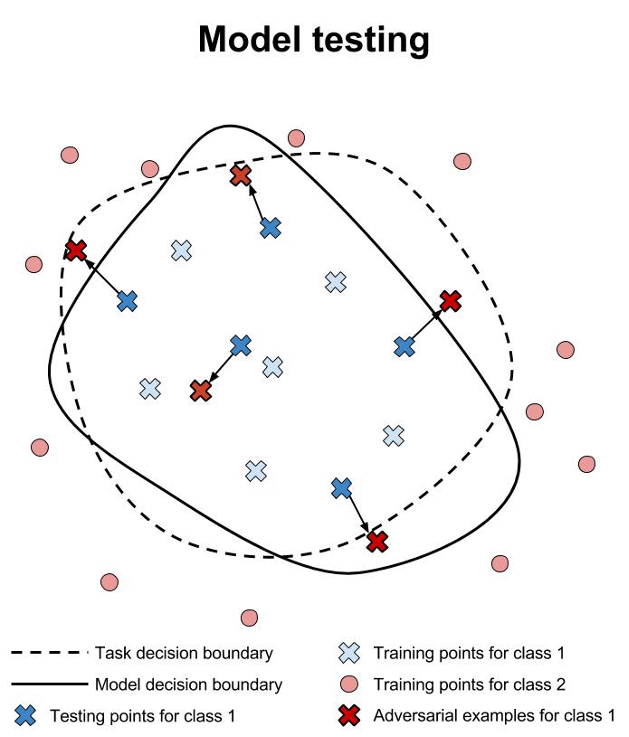
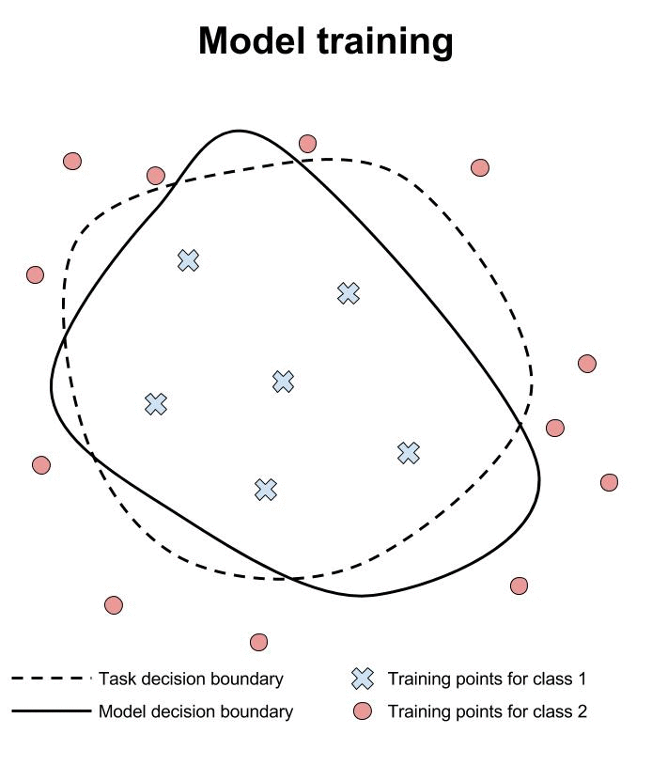
Safety verification for neural networks with provable guarantees. Maximum safe radius.

We have developed a game-based method for formal verification of deep neural networks. In contrast to heuristic search for adversarial examples, verification approaches aim to provide formal guarantees on the robustness of neural network models. This is illustrated above, where we contrast training, testing and verification (images from www.cleverhans.io).

We work with the maximum safe radius problem, which for a given input sample computes the minimum distance to an adversarial example, and demonstrate that, under the assumption of Lipschitz continuity, this problem can be approximated using finite optimisation by discretising the input space, and the approximation has provable guarantees, i.e., the error is bounded. We then show that the resulting optimisation problem can be reduced to the solution of a two-player turn-based game, where the first player selects features and the second perturbs the image within the feature. The method is anytime, in the sense of approximating the value of a game by monotonically improving its upper and lower bounds. We evaluate the method on images and also extend it to videos, where input perturbations are performed on optical flows.

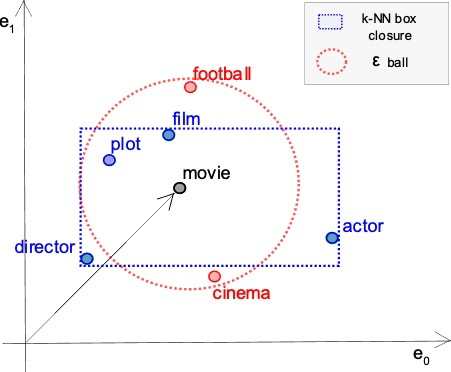
Robustness and explainability of natural language processing (NLP) models. Explanations may fail to be robust.

We study adversarial robustness of NLP models using maximal safe radius computation in the embedding space and formulate a framework for evaluating semantic robustness. We also build on abduction-based explanations for machine learning and develop a method for computing local explanations for neural network models in NLP. These explanations comprise a subset of the words of the input text that satisfies two key features: optimality with respect to a user-defined cost function, such as the length of explanation, and robustness, in that they ensure prediction invariance for any bounded perturbation in the embedding space of the left-out words. Our method can be configured with different perturbation sets in the embedded space (the image shows an example of perturbations in the k-NN neighbourhood and a standard norm ball) and used to detect bias in predictions.

Safe deep reinforcement learning.

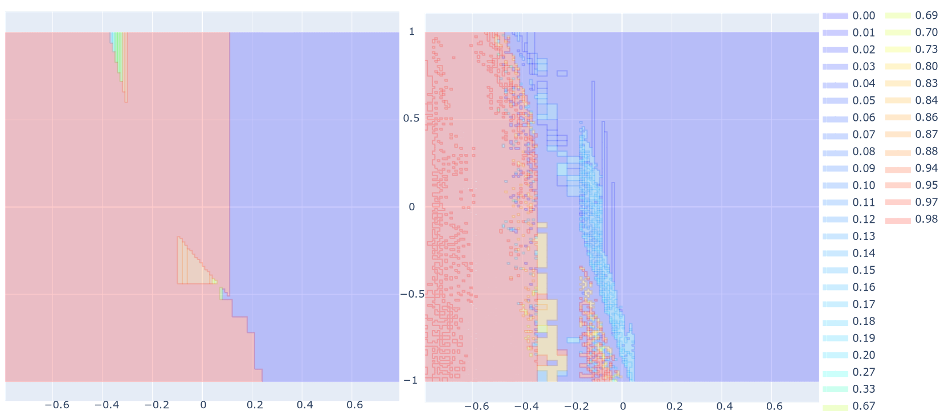
We have developed novel techniques for formally verifying the safe execution of deep reinforcement learning systems. These systems are stochastic due to the possibility of faults, noise or randomised policies, so we synthesise probabilistic guarantees which bound the likelihood of an unsafe state being reached within a specified horizon. To tackle the challenges of continuous state spaces and neural network policy representations, we develop automated methods that construct abstractions as finite Markov processes and then verify them using an extension of PRISM with support for interval-based probabilistic models.

The image shows heatmaps of failure probability upper bounds for subregions of initial states for the pendulum benchmark (x/y-axis: pole angle/angular velocity). Left: the initial abstraction; Right: the abstraction after 50 refinement steps.

Individual fairness guarantees. Certifiable guarantees.

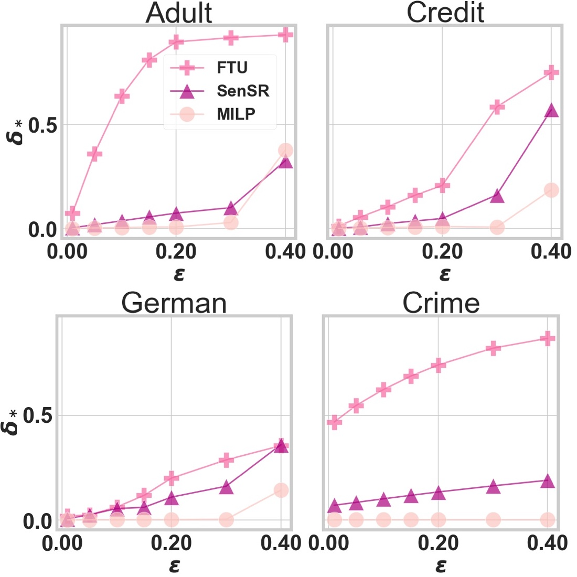
We study certification of fairness for neural networks. Rather than focusing on group fairness, we consider individual fairness, where the decision for any pair of similar individual should be bounded by a maximum decision tolerance. Working with a range of metrics, including the Mahalanobis distance, we propose a method to over-approximate the resulting optimisation problem using piecewise-linear functions to lower and upper bound the neural network’s non-linearities globally over the input space. We encode this computation as the solution of a Mixed-Integer Linear Programming (MILP) problem and show how this formulation can be used to encourage models’ fairness at training time by modifying the loss function.

The image shows certified individual fairness (y axis) as a function of maximum similarity (x axis) on four benchmarks.

Preimage under- and over-approximation for neural networks. Quantitative verification.

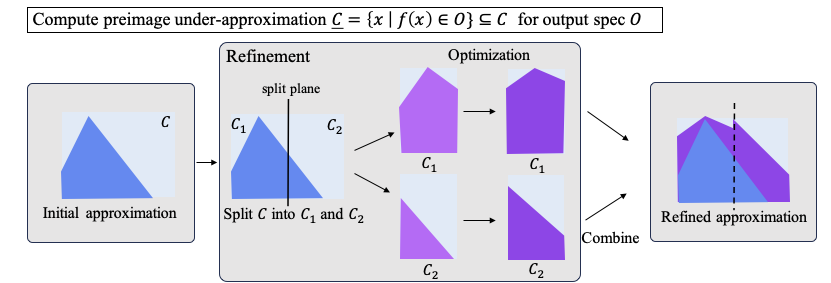
Most methods for neural network verification focus on bounding the image, i.e., set of outputs for a given input set. This can be used to, for example, check the robustness of neural network predictions to bounded perturbations of an input. However, verifying properties concerning the preimage, i.e., the set of inputs satisfying an output property, requires abstractions in the input space. We present a general framework for preimage abstraction that produces under- and over approximations of any polyhedral output set. We evaluate our method on a range of tasks, demonstrating significant improvement in efficiency and scalability to high-input-dimensional image classification tasks compared to state-of-the-art techniques. Further, we showcase the application to quantitative verification, backward reachability for controllers and robustness to patch attacks.

The image illustrates the workflow for preimage under-approximation (shown in 2D for clarity). Given a neural network and output specification O, our algorithm generates an under-approximation to the preimage. Starting from the input region C, the procedure repeatedly splits the selected region into smaller subregions C1 and C2 with tighter input bounds, and then optimises the bounding and Lagrangian parameters to increase the volume and thus improve the quality of the under-approximation. The refined under-approximation is combined into a union of polytopes.

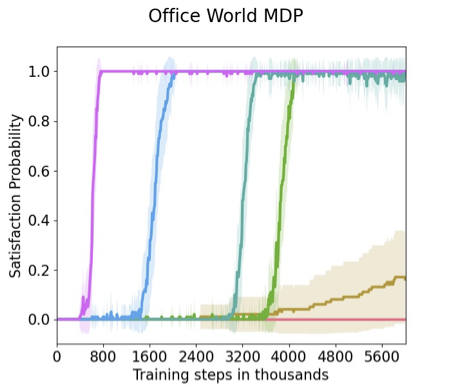
Optimality guarantees for reinforcement learning. Sample efficiency guarantees.

Linear Temporal Logic (LTL) is widely used to specify high-level objectives for system policies, and it is highly desirable for autonomous systems to learn the optimal policy with respect to such specifications. However, learning the optimal policy from LTL specifications is not trivial. We present a model-free reinforcement learning approach that efficiently learns an optimal policy for an unknown stochastic system, modelled using Markov Decision Processes. We propose a novel algorithm, which leverages counterfactual imagining on order to efficiently learn the optimal policy that maximizes the probability of satisfying a given LTL specification with optimality guarantees. To directly evaluate the learned policy, we adopt the probabilistic model checker PRISM to compute the probability of the policy satisfying such specifications.

The image shows the performance of our algorithm (pink) on Office World environment compared to state of the art.

Robustness of Large Language Models (LLMs) for code. Are they robust to semantics-preserving code mutations?

Understanding the reasoning and robustness of LLMS is critical for their reliable use in programming tasks. While recent studies have assessed LLMS’ ability to predict program outputs, most focus solely on the accuracy of those predictions, without evaluating the reasoning behind them. Moreover, it has been observed on mathematical reasoning tasks that LLMS can arrive at correct answers through flawed logic, raising concerns about similar issues in code understanding. In this work, we evaluate whether state-of-the-art LLMS with up to 8B parameters can reason about Python programs or are simply guessing. We apply four semantics-preserving code mutations: renaming variables, mirroring comparison expressions, swapping if-else branches, and converting for loops to while. We evaluated six LLMS and performed a human expert analysis using LIVECODEBENCH to assess whether the correct predictions are based on sound reasoning. We also evaluated prediction stability across different code mutations on LIVECODEBENCH and CRUXEVAL. Our findings show that LLMS trained for code produce correct predictions based on flawed reasoning for 10% to 50% of cases. Furthermore, LLMS often change predictions in response to our code mutations, indicating they do not yet exhibit stable, semantically grounded reasoning.

The image shows an example prompt provided to the LLM.