


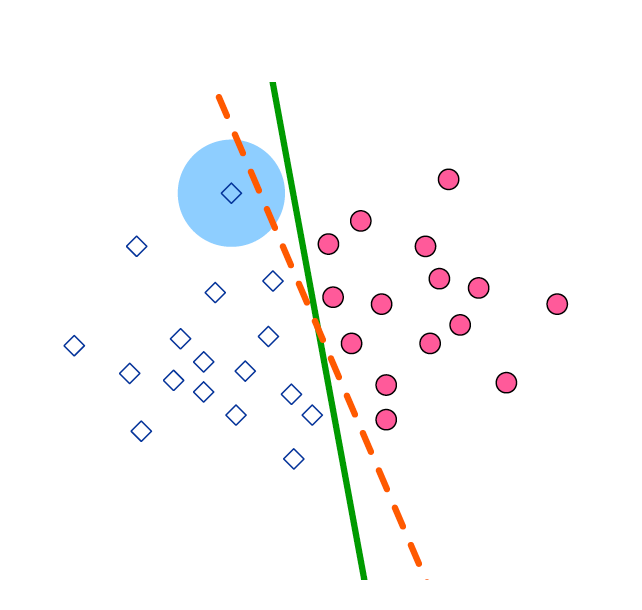
The Safety, Robustness and Fairness Guarantees theme is focusing on robustness evaluation of trained machine learning models on a given input, through developing algorithmic techniques that compute how the output of the model changes if the input is corrupted at test time by a bounded adversarial perturbation. This is known as an evasion attack. For classifiers, the label of the input and its corrupted instance are usually assumed to be the same, and this concept of robustness is known as 'constant-in-the-ball' risk. An alternative notion of robustness for evasion attacks considers the problem of robustly learning a model where there exists a ground truth label. In this setting, which is known as ‘exact-in-the-ball’ robustness (shown in the image on the right), the model’s label for a perturbed data point is compared to the ground truth rather than the uncorrupted point’s label. In this project we initiated a study of efficiently learning robust models, which focused on sample complexity of PAC learning under various assumptions on the power of adversary and distributions of the data. The advantage of this approach is that robustness is guaranteed through the learning process as long as these assumptions are satisfied. However, a fundamental understanding of the interplay between the different assumptions must be developed for simpler settings before these methods can be considered for complex machine learning models such as neural networks.
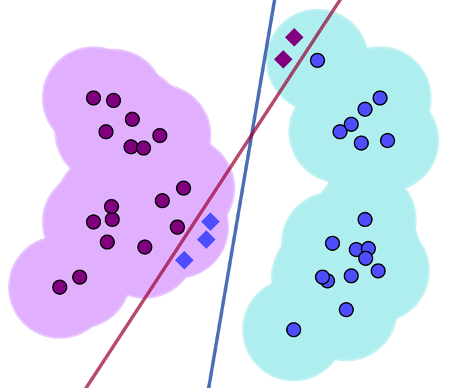
We study, for the first time, the feasibility and efficiency of robust learning against evasion attacks from the computational learning theory standpoint to address the provably correct synthesis goal for machine learning components. A surprising observation was the impossibility of robust learning of any concept under distributional assumptions. The work has focused on seeking results that ensure efficiency of robust learning by imposing appropriate distributional assumptions and bounding the adversary’s power.
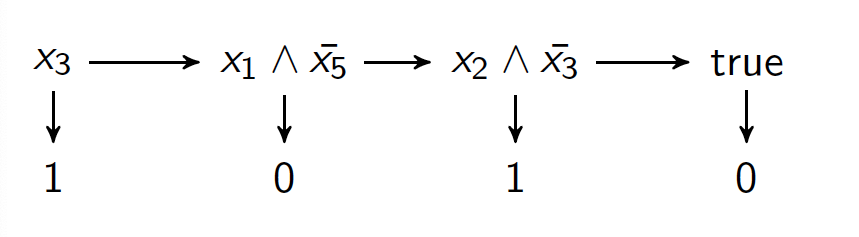
Since then, the work has focused on seeking results that ensure efficiency of robust learning by imposing appropriate distributional assumptions and bounding the adversary’s power, enabling generalisation to further concept classes. We have shown that the adversarial budget is a fundamental quantity in the sample complexity of robust learning against evasion attacks. In particular, decision lists (illustrated in the image) can be efficiently robustly learned under smooth distributions if the budget is log(n), where n is the dimension of the input space (we focus on the Boolean hypercube). This implies that we can use standard PAC algorithm as a black box.