FUN2MODEL Research Themes:
Tractable Causal Inference and Reasoning
« Overview
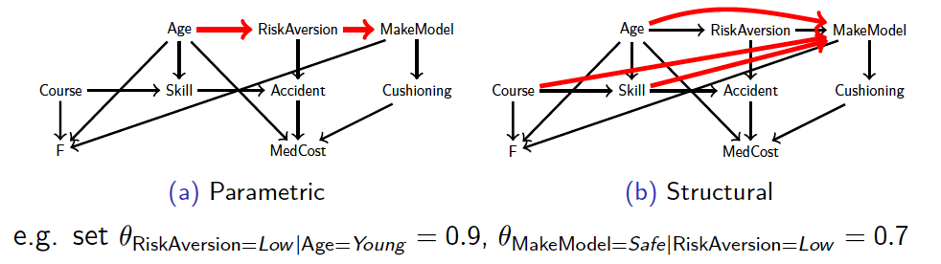
Robustness to causal interventions. Distribution shifts.
Robustness of decision rules to shifts in the data-generating process is crucial to the successful deployment of decision-making systems, since they have to be applied to input points outside of the data distribution they were trained on. Local adversarial robustness guarantees that the prediction does not change in some vicinity of a specific input point, whereas we are instead interested in distribution shifts. Such shifts can be viewed as interventions on a causal graph, which capture (possibly hypothetical) changes in the data-generating process, whether due to natural reasons or by the action of an adversary.
The diagram shows a causal Bayesian network of an insurance model under two types of such shifts, parametric (change of conditional probability values) and structural (removal/addition of causal links).
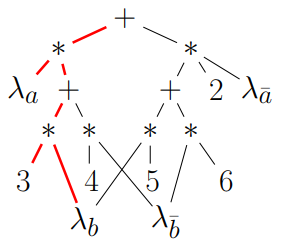
Interventional robustness via arithmetic circuits. Provable guarantees.
We formally define the interventional robustness problem, a novel model-based notion of robustness for decision functions that measures worst-case performance with respect to a set of interventions that denote changes to parameters and/or causal influences. While the problem itself is exponential, by relying on a tractable representation of Bayesian networks as arithmetic circuits, also in the presence of data uncertainty, we provide efficient algorithms for computing guaranteed upper and lower bounds on the interventional robustness probabilities. To this end, we exploit the efficient compilation of Bayesian networks into arithmetic circuits (see image), and compile the decision function and the data-generating process jointly.
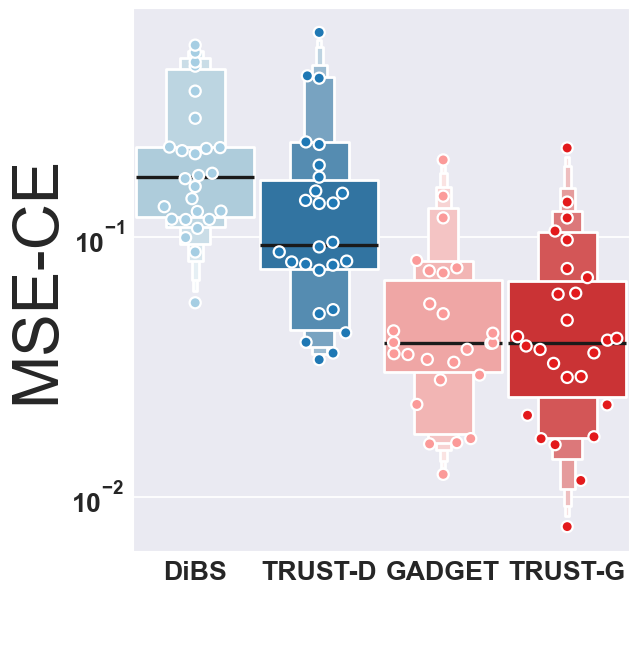
Tractable structure learning via product-sum networks.
Bayesian structure learning allows one to capture uncertainty over the causal directed acyclic graph (DAG) responsible for generating given data. We develop a TRUST (Tractable Uncertainty for STructure learning) framework, which supports approximate posterior inference that relies on probabilistic circuits as the representation of posterior belief. In contrast to sample-based posterior approximations, our representation can capture a much richer space of DAGs, while being able to tractably answer a range of useful inference queries. We empirically show how probabilistic circuits can be used as an augmented representation for structure learning methods, leading to improvement in both the quality of inferred structures and posterior uncertainty, and show how causality queries can be estimated.
The image shows MSE (Mean Squared Error) of Causal Effects (lower is better) for TRUST in comparison with state of the art.
Sort by: date, type, title
12 publications:
-
[SBK25]
Daqian Shao, Thomas Kleine Buening, Marta Kwiatkowska.
A Unifying Framework for Causal Imitation Learningwith Hidden Confounders.
In Workshop on Spurious Correlation and Shortcut Learning: Foundations and Solutions, Workshop at The International Conference on Learning Representations (ICLR) 2025.
2025.
[pdf]
[bib]
https://arxiv.org/abs/2502.07656
-
[SSQK24]
Daqian Shao, Ashkan Soleymani, Francesco Quinzan, Marta Kwiatkowska.
Learning Decision Policies with Instrumental Variables through Double Machine Learning.
In Proc. 41st International Conference on Machine Learning (ICML 2024).
2024.
[pdf]
[bib]
https://arxiv.org/abs/2405.08498
-
[WK23]
Benjie Wang and Marta Kwiatkowska.
Compositional Probabilistic and Causal Inference using Tractable Circuit Models.
In Proc. 26th International Conference on Artificial Intelligence and Statistics (AISTATS).
2023.
[pdf]
[bib]
-
[QSJ+23]
Francesco Quinzan, Ashkan Soleymani, Patrik Jaillet, Cristian R. Rojas, Stefan Bauer.
DRCFS: Doubly Robust Causal Feature Selection.
In ICML2023 Fortieth International Conference on Machine Learning. To appear.
2023.
[pdf]
[bib]
-
[WWK22c]
Benjie Wang and Matthew Wicker and Marta Kwiatkowska.
Tractable Uncertainty for Structure Learning.
In 5th Workshop on Tractable Probabilistic Modelling (TPM). This paper was accepted for ICML 2022.
2022.
[pdf]
[bib]
-
[WK22]
Benjie Wang and Marta Kwiatkowska.
Symbolic Causal Inference via Operations on Probabilistic Circuits.
In NeurIPS Workshop on Neuro Causal and Symbolic AI (nCSI'22).
2022.
[pdf]
[bib]
-
[WWK22]
Hjalmar Wijk, Benjie Wang and Marta Kwiatkowska.
Robustness Guarantees for Credal Bayesian Networks via Constraint Relaxation over Probabilistic Circuits.
In Proc. 31st International Joint Conference on Artificial Intelligence (IJCAI'22). To appear.
July 2022.
[pdf]
[bib]
-
[WWK22b]
Benjie Wang, Matthew Wicker and Marta Kwiatkowska.
Tractable Uncertainty for Structure Learning.
In Proc. 39th International Conference on Machine Learning (ICML'22). To appear.
July 2022.
[pdf]
[bib]
-
[WLK21]
Benjie Wang, Clare Lyle and Marta Kwiatkowska.
Provable Guarantees on the Robustness of Decision Rules to Causal Interventions.
In 30th International Joint Conference on Artificial Intelligence (IJCAI'21).
August 2021.
[pdf]
[bib]
Sort by: date, type, title
« Overview





